Deret Fibonacci, dinamai menurut ahli matematika Italia Leonardo Fibonacci, adalah urutan angka tak terbatas yang telah memikat ahli matematika, ahli biologi, seniman, dan filsuf selama berabad-abad. Ini muncul secara misterius dalam berbagai konteks ilmiah dan alam dan telah menjadi lambang keindahan matematika tak terduga yang ditemukan di alam.
Memahami Deret Fibonacci
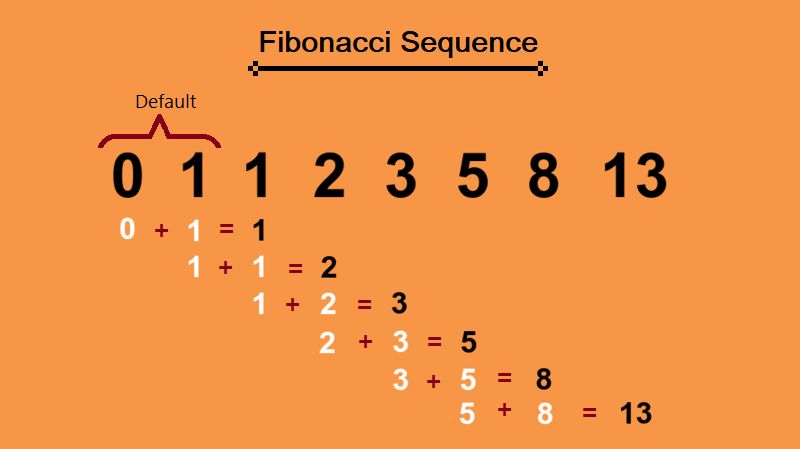
Secara paling sederhana, deret Fibonacci adalah serangkaian angka di mana setiap angka setelah dua yang pertama adalah penjumlahan dari dua yang sebelumnya. Seringkali mulai dari 0 dan 1, deretnya menjadi: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, dan seterusnya.
Ditulis secara matematis, deret tersebut didefinisikan dengan relasi perulangan berikut:
F( 0) = 0,
F(1) = 1,
F(n) = F(n-1) + F(n-2) untuk n > 1123F(0)=0,F(1)=1,F(n)=F(n-1)+F(n -2)forn>1
Sifat rekursif deret Fibonacci berarti bahwa setiap suku dalam deret tersebut berhubungan langsung dengan dua suku sebelumnya. Properti ini menjadikannya alat penting dalam berbagai masalah matematika dan komputasi.
Seri Fibonacci di Alam dan Sains
Selain minat matematisnya yang murni, deret Fibonacci memiliki aplikasi menarik dalam ilmu alam dan biologi. Tampaknya dalam berbagai aspek alam:
Phyllotaxis: Banyak tumbuhan menunjukkan urutan Fibonacci dalam susunan daun di sepanjang batang, yang mengoptimalkan paparan sinar matahari dan hujan. Reproduksi kelinci: Ini sebenarnya masalah yang memperkenalkan deret Fibonacci. Fibonacci mengajukan dan memecahkan masalah dalam “Buku Perhitungan” yang melibatkan pertumbuhan populasi kelinci berdasarkan asumsi ideal. Biji pinus dan nanas: Spiral pada biji pinus dan nanas mencerminkan angka Fibonacci. DNA: Urutan Fibonacci juga muncul dalam struktur DNA, dengan satu putaran lengkap heliks ganda berukuran panjang 34 angstrom dan lebar 21 angstrom (keduanya bilangan Fibonacci).
Ini hanya beberapa dari banyak contoh di mana deret Fibonacci muncul di alam.
Deret Fibonacci dalam Ilmu Komputer dan Algoritma
Deret Fibonacci juga memainkan peran penting dalam ilmu komputer. Algoritma untuk menghitung angka Fibonacci digunakan untuk mengajarkan dasar-dasar pemrograman, rekursi, pemrograman dinamis, dan efisiensi algoritme.
Berikut adalah program Python sederhana untuk menghasilkan deret Fibonacci hingga n:
def fibonacci(n):
fib_sequence = [0, 1]
sementara len(fib_sequence) <n:
fib_sequence.append(fib_sequence[-1] + fib_sequence[-2])
mengembalikan fib_sequence
# Cetak 10 angka pertama dalam deret Fibonacci
Cetak (fibonacci (10)) 12345678Deffibonacci (n): fib_sequence = [0,1] whilelen (fib_squence) <n: fib_sequence.append (fib_sefeseence [-1]+fib_squence [-2]) returnfib_sequence# cetak 10 angka pertama dalam angka pertama dalam angka pertama dalam 10 angka pertama dalam fib_squence [-2]) deret Fibonaccicetak(fibonacci(10))
Kode ini dimulai dengan daftar yang berisi dua angka Fibonacci pertama, 0 dan 1. Kode ini kemudian memasuki lingkaran, yang berlanjut hingga panjang daftar adalah jumlah suku yang diminta. Pada setiap iterasi loop, ini menghitung angka Fibonacci berikutnya dengan menambahkan dua angka terbaru dalam daftar, lalu menambahkan angka ini ke akhir daftar.
Ketika Anda menjalankan kode ini dengan argumen 10, kode ini akan mencetak: [0, 1, 1, 2, 3, 5, 8, 13, 21, 34], yang merupakan 10 angka pertama dalam deret Fibonacci.
Kesimpulan
Deret Fibonacci adalah deret angka sederhana dengan kompleksitas dan kegunaan yang tidak terduga. Interaksinya antara teori bilangan, sifat, dan komputasi memberikan bukti yang luar biasa tentang keterkaitan konsep matematika. Baik Anda menghitung kelopak bunga, mengoptimalkan algoritme komputer, atau sekadar menikmati keindahan matematis, deret Fibonacci terus memikat pikiran dengan banyak cara yang menarik.
Referensi tecadmin.com